都市間ネットワーク構造が感染拡大に及ぼす影響について
2020/9/18
※2021年7月1日付の社名変更に伴い、TRC EYEはTokio dR-EYEに名称が変更となりました。
都市間ネットワーク構造が感染拡大に及ぼす影響について - TRC EYEPDF
矢野 良輔
企業財産本部 上級主任研究員
COVID-19 が世界中に蔓延して、半年以上が経過した現在、国内では目下、第 2 波の傘下にあると考えられている．国内における観光業などのサービス産業へのダメージを抑えるために、国は、Go To トラベルキャンペーンを打ち出したものの、都内における感染増加に伴い、急遽、東京都をキャンペーンから除外するなどの、緊急対応を行った．
一般的に、感染拡大は、ヒト－ヒト接触で起こると考えるので、これを減らすことは、大原則であるが、経済を回すという意味においては、完全な個人レベルでの外出自粛は、かなり困難な状況下にある． 特に、接触時間が長くなる飲食店での接触は、一人の感染者が 10－20 人に感染をさせてしまう、スーパースプレッダーになる可能性があることが、危惧されている．
感染拡大は、このように極めて局所的空間において短時間で起きるものであるので、これを律儀にモデル化したシミュレーションを行う事には一定の困難が伴う．また、この時空間の局所性が、長時間、大空間での感染の拡大に効果を持つものであれば、感染拡大は様々な時空間スケールが混在する複雑系の現象であると言える．
これまで、感染拡大のシミュレーションに使われてきたモデルは、SIR(Susceptible-Infected-Recovered)モデルという、平均場理論に立脚した 100 年ほど前のモデルである．この SIR モデルの制御パラメタは、感染率と回復率の 2 個しかないために、SIR モデルを解いた結果を用いて実データをフィッティングするには不十分であることは、並木らの考察で示されている．そこで、並木[2]は、小田垣[1]の SIQR (Susceptible-Infected-Quarantined-Recovered)モデルによる実データのフィッティングを提案している．ここで、コントロールパラメタとして、総人口を実効感染機会人口として再定義することで、実データを見事にフィッティングする方法を考案している．
この並木の SIQR モデルを使った方法は、各都道府県の感染者数の時系列的変化を第 1 波、第 2 波の途中まで上手く再現できるモデルであることは、SIQR モデルのような平均場理論で複雑系の現象である感染拡大が局所的に再現できることを示唆している．
一方で、並木の方法は、データ駆動型の制御パラメタ推定の形式をとるために、一定期間データを蓄積して上で、SIQR モデルのシステム同定を行う必要があり、初期における挙動や発生の予測をすることは、難しい．このような、初期の感染者数の立ち上がりを予測するには、何時、何処で感染の種が撒かれたかを知っておく必要がある．この感染の種の撒かれ方は、ひとえに、感染者の移動に依存する部分であり、これを正確に把握することは、難しい側面もある．
そこで、本稿では、人の移動が、感染者拡大にどのような影響を及ぼし得るのかを、総務書統計局が公開している日本全国 1898 都市について、ネットワーク構造を導入し、簡単な考察をしてみる．此処でいう、ネットワークの作り方においては、決定論的な方法は無いものの、幾つかのシナリオに応じた都市間ネットワークを作成し、そこでの感染拡大について、思考実験を行う．利用するモデルは小田垣－並木の SIQR モデルとして、パラメタセットは、簡単のために全ての都市で一定に固定する．故に、得られた結果は、実データを再現するように設定されていないことは、強調しておく．
参考までに、未感染者数:=S, 感染者数:=I, 隔離者数:=Q, 回復者数:=R、接触感染率:=β, 感染者との接触時の感染者隔離率:=q’, 接触後の感染者隔離率:=q, 未隔離感染者の回復率:=γ, 隔離感染者の回復率:=γ’として、小田垣－並木の SIQR モデルは、次のように書かれる．
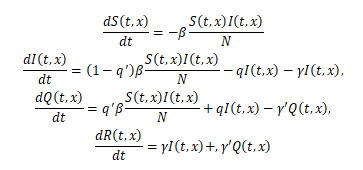
t は時間、x は、場所を表している．N は、実効感染機会人口として、制御パラメタである．制御パラメタセット(β, q, q’, γ, γ’, N)は、並木の方法では、実データをフィッティングするように決定されているが、ここでは、簡単のために定数としておく．上式では、人の出入りは、加味されていないので、地点 x から地点 y への人の移動を考慮して上式を書き直すと、
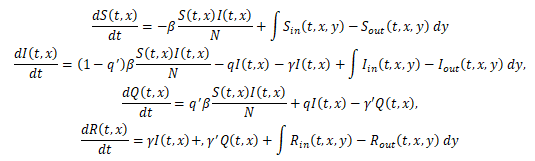
と書くことが出来る．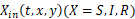 
は、ある時刻 t に、y から x へ移動する属性 X の人数であり、 
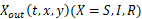は、ある時刻 t に、x から y へ移動する属性 X の人数である．
上式では、空間を連続としているが、離散的な都市ネットワークを考えるならば、積分を Σ に書き換えれば良い．
1898 都市データに対して、都市間ネットワークを作る上で、先ずは、都市間の距離に応じてリンクを張るとしておくと、図 1 に示すように、
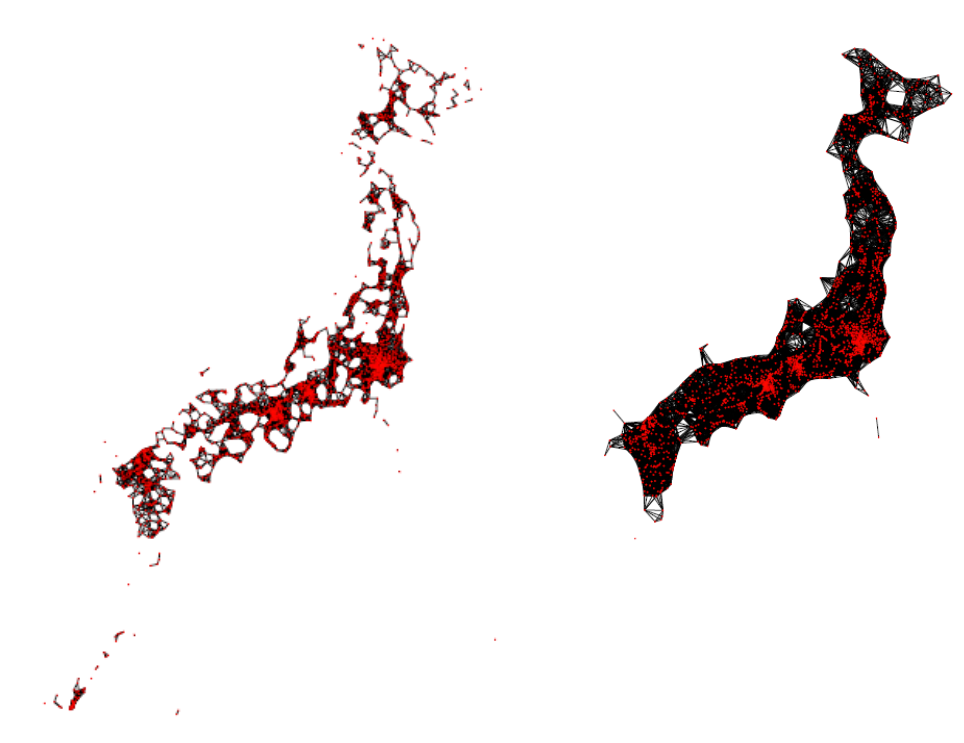
図 1：リンクの最大距離を 30km とした時の都市間ネットワーク(左図)と、30km とした時の都市間ネットワーク(右図)
都市間の最大距離を 30km とすると、ネットワーク構造は極めてスパースなものになるが、60km とすると、ネットワーク構造はかなり密に変化している．都市間の最大リンク距離を DT[km]として、スモールワールド性(異なる都市間のネットワーク近接性)の指標となるクラスタ係数(ネットワークによってできる三角形の数を全結合ネットワークで出来る三角形の数で割ったもの)を計算すると、図 2 の様になり、シグモイド関数のような形状が得られ、リンクの最大距離が 2000km になると、ほぼ全結合ネットワークになることが解る．DT(200km 以下)が小さい範囲では、クラスタ係数は DTの指数関数で増加する．図1 のような状態は、つまり、移動距離制限をかけた自粛状態に相当しており、東京－大阪などの大都市間を直接移動するようなリンクは存在しない．
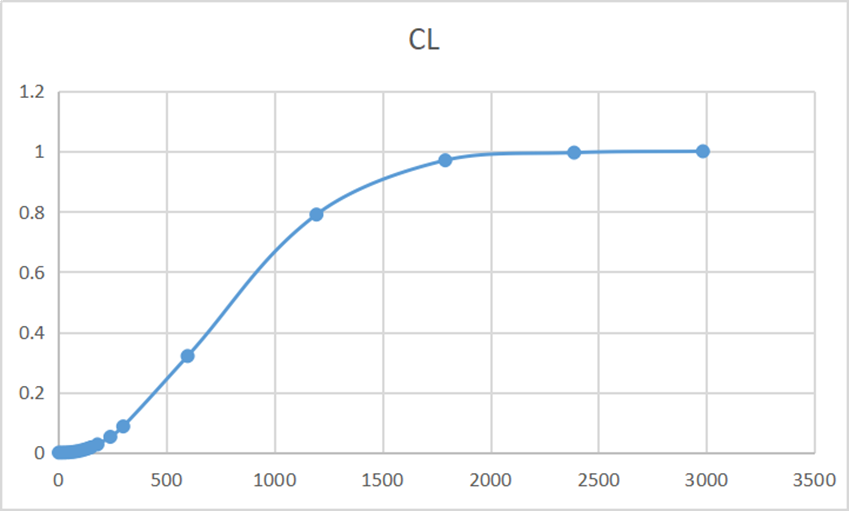
図 2：リンクの最大距離とクラスタ係数の関係
ネットワーク構造をもう少し調べておくと、１都市(1 ノード)に接続するリンク数の分布関数を以下に定義しておくと、
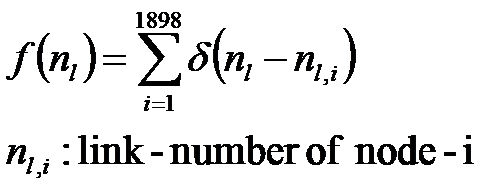
DT=30km, 60km, 120km の時の、リンク数の分布関数は、図 3 の様になる．
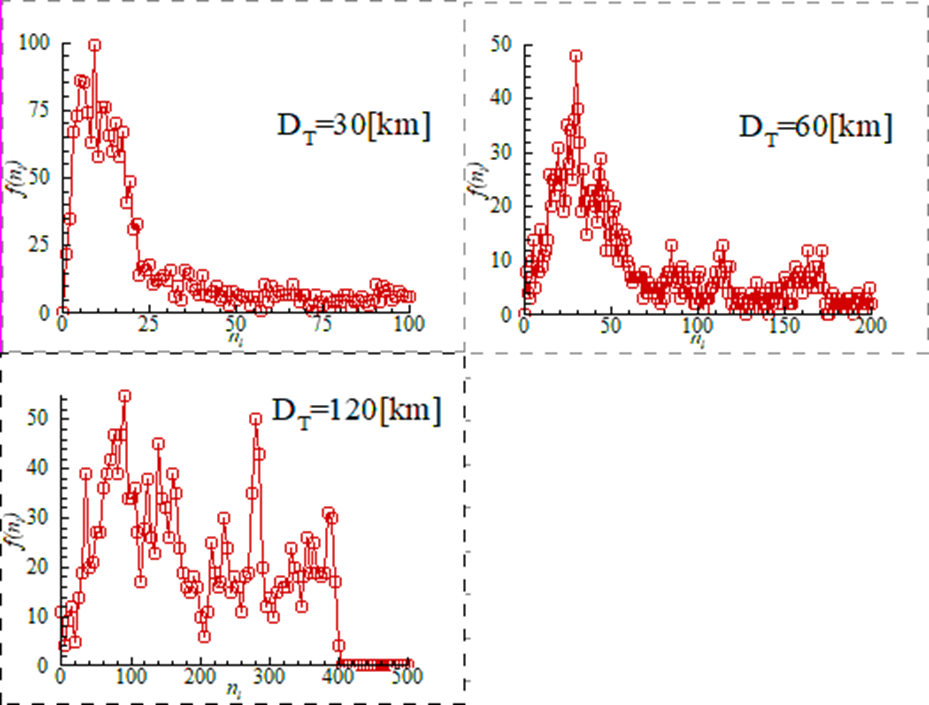
図3：f(nl)とnlの関係DT=30km(左上)、DT=60km(右上)、DT=120km(左下)
図3が示すように、DT=30kmでは、べき乗のファットテイルを持つ、ガンマ分布に似た形状になり、DT=60kmでは、コーシー分布に似た鋭いピークを、リンク数25本周辺に持つ分布となる．一方で、DT=120kmでは分布は平坦になり、際立った構造を持っていない．つまり、DT=30km, 60kmでは、スケールフリーネットワーク構造を持つことが解るが、これは、多くのノードが、東京、名古屋、大阪といった中心地に近距離で集中していることに起因している．
次に、DT=30km, 60kmでの感染拡大について、考えてみる．初期条件として、東京都新宿区の1%が感染しており、他のノードでの感染者は居ないものとする．次に都市間を移動する人流であるが、ここでは、簡単のためにノードiの人口をNiとして、属性をS,I,Rとしておくと、ノードiでの属性S,I,Rの流出入 は、白色ノイズを用いて次式に書かれる．
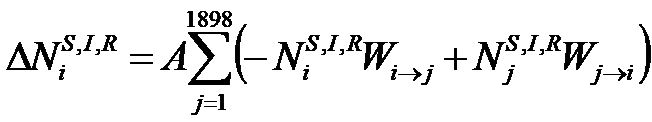
上式で、Aは、正の定数ですべての拠点で同じ値を用いている．上式では、ノード間の移動、i→j→i(文京区から千代田区から文京区、のように通勤に伴うような人流)を表現できないので、人口の多いノードから、少ないノードに継続的に人が流出してしまうモデルになっている．
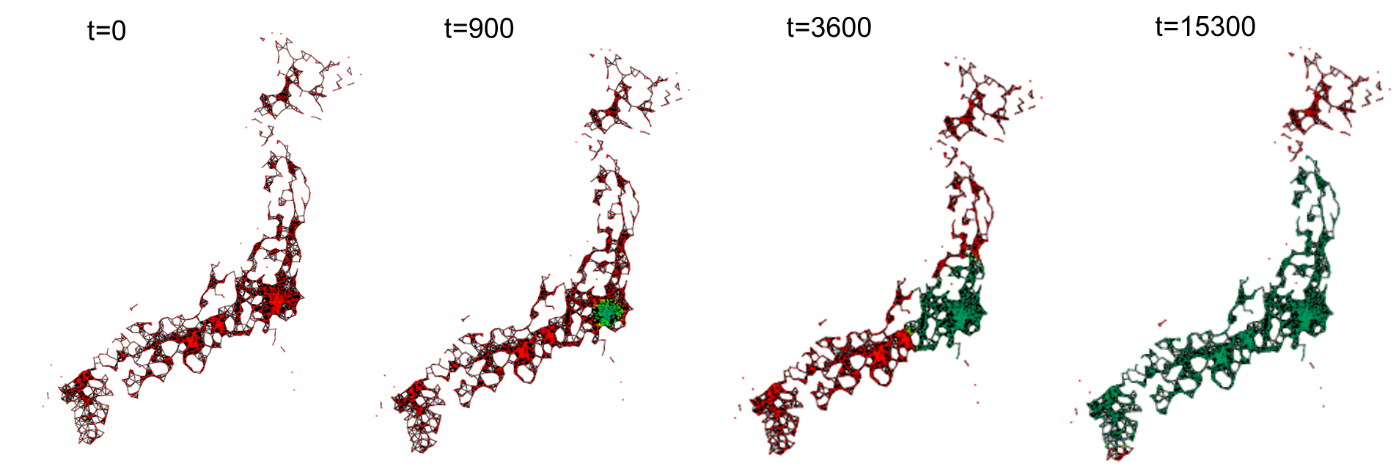
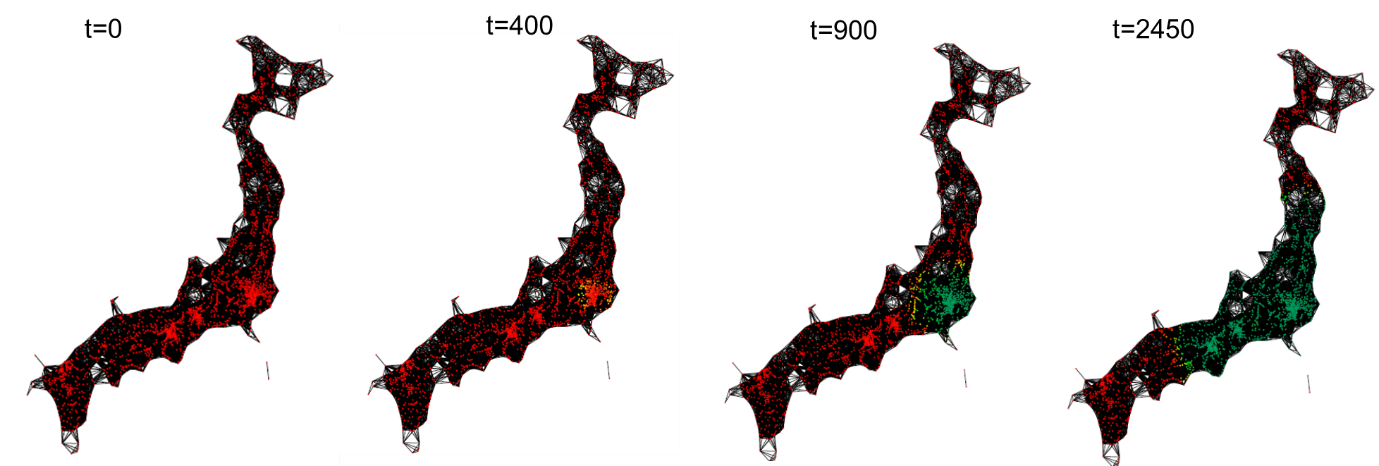
図4：未感染者の分布率(S/(S+I+Q+R))の時間推移．ノードが赤いほど1に近く、青いほど0に近い(上図：DT=30km, 下図：DT=60km)
図4が示す通り、DT=60kmの時の感染拡大の速度は、DT=30kmに比べて早いことが解る．これは、より多くのノードがつながることが、感染拡大の空間伝播速度を上げていることを示している．
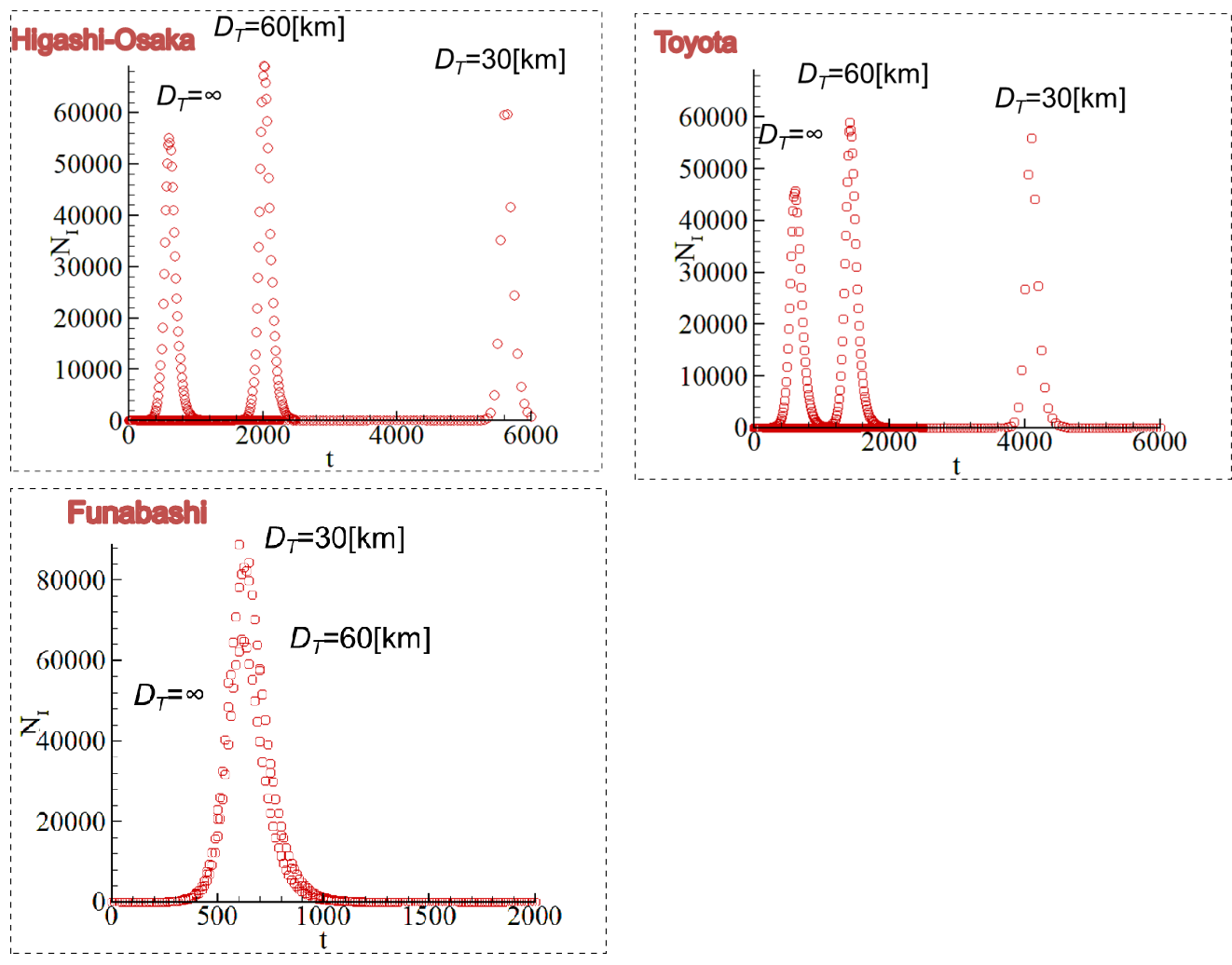
図 5: 感染者数の時間推移（左上：東大阪市、右上：豊田市、左下：船橋市）
図5は、大阪府東大阪市、愛知県豊田市、千葉県船橋市での感染者数の推移を表している．DT=∞は、全結合ネットワークに相当している．予想通り感染者の増加が開始する時間は、DT=∞, 60km, 30km の順に早い．一方で、船橋市では、新宿区に近いこともあり、DT により感染開始時間の差は著しくない．
最後に、東京から、各都市に人が移動する影響を考えてみる．テストケースとして次の 2 ケースを考察してみる．
Case A: DT=30km で作成したネットワークに、東京駅から 12km 圏内に存在するノードから、20 万人以上の人口を有するノードにリンクを張ることで出来るネットワークを重ねる．
Case B: DT=30km で作成したネットワークに、東京駅から 12km 圏内のノードから、ランダムにある確率で、リンクを張ることで出来るネットワークを重ねる．
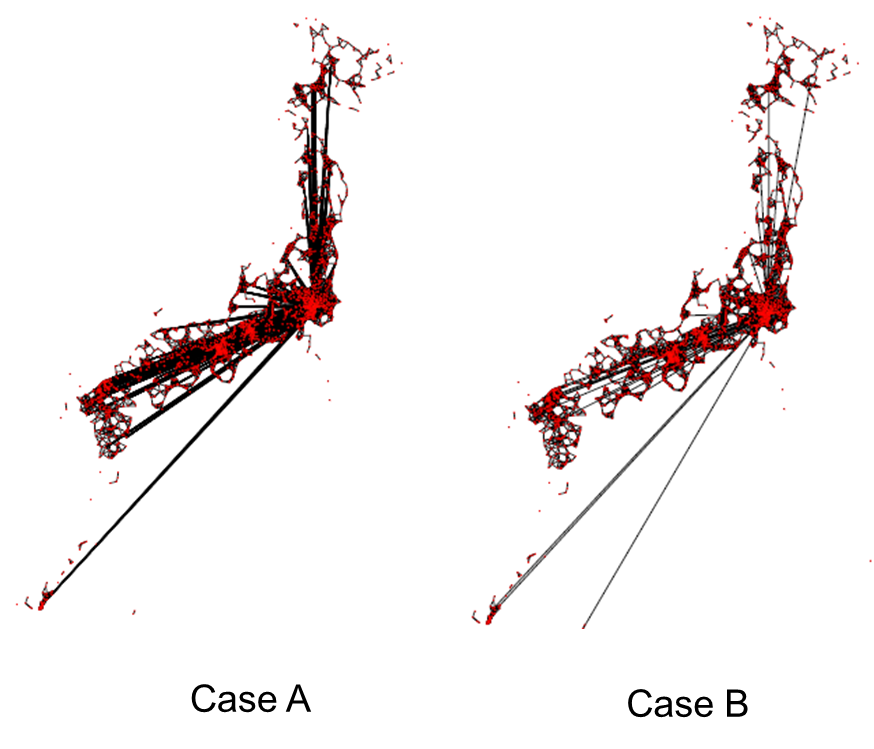
図6: Case A, Bのネットワーク構造の可視化
当然、Case A も B も東京の中心地から各都市への移動が増える分、感染拡大速度は、大きくなると予想される．
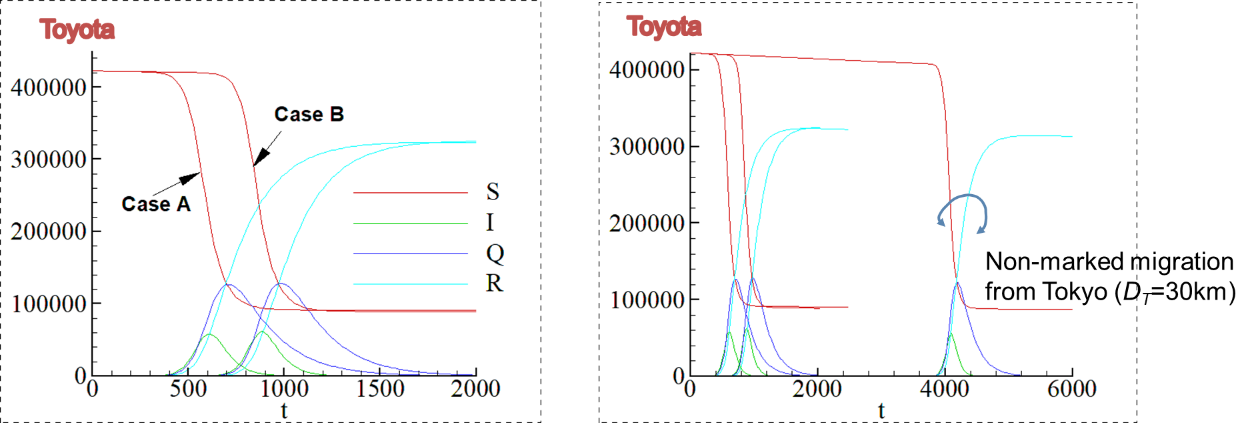
図 7: 豊田市での SIQR 人口の時間推移(左図: Case A+B の結果、右図、Case A+B の結果と DT=30km で作られたネットワークによる結果)
図７に示すように、Case A における感染開始時間は、Case B よりも早い．これは、大都市間がつながるほど、感染の空間拡大速度は、大きくなることを意味している．但し、ここで最も重要なことは、SIQR人口は、ネットワーク構造の変化に殆ど影響されないという事である．つまり、ネットワーク構造の違いにより異なるのは、感染者が増えてくる時刻のみである．このように、SIQR モデルのコントロールパラメタを一端固定してしまえば、感染者数の増減は、人流の影響を大きく受けないことになってしまう．並木の結果によると、SIQR モデルのコントロールパラメタは、感染の中盤に人流を増減させてもほとんど変化しないという結果を得ているが、本稿の結果においても、人流の効果が定量的な感染者の増減へ与える影響は、時間軸のみということになる．これは、あるノードに感染者が一人でも入り込めば、SIQR モデルの性質上、パラメタの値に応じて、増加していく事とも関係している．
しかし、ここで、注意すべきは、ロックダウンのようなものは、人流を規制するというよりも、むしろ市内地域活動を制限し、接触率を下げることに繋がる可能性があるという点である．故に、小規模なロックダウンが何も効果が無いと結論付けることは、本稿の目的ではない．むしろ、本稿の主張は、人の都市間の移動制限が、感染者増加開始を遅らせることが出来るという点である．ワクチンの完成までに、我々が時間稼ぎを目論むのであれば、移動制限には一定の効果があるものと結論付けたい．
謝辞：
本稿は、一色浩(数理解析研究所所長)、木下健(東大名誉教授)、梶原宏之(九大名誉教授)、鈴木基光(元日立造船)、古寺雅晴(大阪産技総研理事長)、並木正夫(元東芝副社長)の各氏で進めている新型コロナウィルス研究会[3]での議論を通して作成されている．特に、並木正夫氏には沢山貴重な計算結果を共有いただき、感謝申し上げる． また、SIQR モデルが示唆する PCR 検査の重要性については、https://note.com/antivirus/n/n45e80a99f6baにある並木氏の note（ノート）に詳しいので、参照されたい．また、ローカルロックダウンの効果については、木下と一色[4]を参照されたい.
追記：
9 月 2 日現在では、感染者数は 8 月下旬より減少傾向にあり、全国的には、第 2 波のピークを過ぎたようにも見受けられる．しかし、これは、国民一人一人の一定の行動制限の帰結であることも忘れてはならない．本稿では、感染拡大初期段階での感染者数の増加が、その後の感染拡大ピークに主たる影響を及ぼすことに言及したものの、これは、一定の行動制限が継続している場合の話である．故に、我々が再度、行動制限を解き、ヒト－ヒト接触の機会をむやみに増やすことは、得策ではない．というのも、感染初期から現在までの感染者の時系列変化も、行動無制限への移行により、より大きな波の一部であったという事になりかねないからである．つまり、「感染の時系列変化はフラクタルのようなものだと考えた方が無難である」ことは、先述の通り、「感染拡大問題は様々な時空間スケールが混在した複雑系の物理と考えるべき問題である」こととも無関係ではない．また、スーパースプレッダーの存在は、SIR 系モデルが予測する指数関数的感染者の減衰ではなく、時系列的現象が、ロングテイルとなることを示唆する事から、次の波を駆動する因子となり得ることに留意しなければならない．今後の課題としては、第 N 波と第 N+1 波の時間間隔を含めて、複数の感染の波を計算できることが望まれるが、そのモデルは、並木らにより、現在、モデルが提案済みであり、別の機会に触れることとする．
参考情報
執筆コンサルタント
矢野 良輔
企業財産本部 上級主任研究員
参考文献
[1] 小田垣孝、新型コロナウイルスの蔓延に関する一考察、物性研究電子版 Vol. 8, No. 2 （2020・05）, pp. 1-10
[2] 並木正夫、新型コロナ第 2 波感染の予測～ SIQR モデルとその係数の決め方
https://note.com/antivirus/n/n45e80a99f6ba
[3] 新型コロナウィルス研究会 https://note.com/antivirus
[4] 木下健、一色浩、ローカルロックダウン効果の予測可能性と課題に関する一考察
https://note.com/antivirus/n/n45e80a99f6ba